O leitor que já estudou Cálculo Diferencial e Integral provavelmente concorda que, no estudo desta disciplina, as interpretações geométricas de vários conceitos desempenham um papel bastante significativo. É de se notar, entretanto, que na hora de se estudar a prova do Teorema Fundamental do Cálculo (TFC), o apelo geométrico parece se desvanecer e a abordagem que geralmente se vê é essencialmente analítica. Mas será que existe algum tipo de interpretação geométrica para a demonstração do TFC? Tal interpretação não só existe como consiste numa das primeiras provas já publicadas deste importante resultado.
Esta postagem tem, então, o objetivo de expor uma demonstração geométrica para o 1º Teorema Fundamental do Cálculo (aqui, "1º teorema" refere-se à parte de acordo com a qual "a derivada da integral de uma função é a própria função").
Notadamente, apresentaremos o argumento devido ao matemático inglês Isaac Barrow (1630-1677) publicado em 1669 na sua obra Geometrical Lectures (Proposição 11, Lecture X).

Isaac Barrow
Cabe notar que, nos livros de cálculo, geralmente o TFC versa sobre uma função contínua $f:[a,b]\to\mathbb{R}$ (na realidade, bastaria $f$ ser integrável, conforme se vê nos curso de análise). Porém, na nossa exposição, exigiremos (assim como Barrow o fez) um pouco além da continuidade de $f$. Especificamente, suporemos $f$ positiva e crescente (o leitor notará que o mesmo argumento vale para uma função negativa, mas não vale para os casos em que $f$ se anula nalgum ponto).
Seja, então, $f:[a,b]\to\mathbb{R}$ uma função contínua, positiva e crescente. Considere a função $F:[a,b]\to\mathbb{R}$ dada por
$$F(x)=\int_a^x f(s) ds.$$
Geometricamente, $F(x)$ representa a área da região limitada pelo gráfico de $f$ e pelo eixo das abscissas entre os pontos $a$ e $x$ (veja figura 1). Para fins de ilustração, suporemos $a>0$ e $F(x)>f(x)$ para todo $x\in[a,b]$.

Figura 1: geometricamente $F(x)$ corresponde à área da região sombreada.
Marquemos o ponto $t=x-\tfrac{F(x)}{f(x)}$ sobre o eixo das abscissas e tracemos a reta $R$ que intersecta o eixo das abscissas no ponto $ t $ e passa pelo ponto $(x,F(x))$ (veja figura 2). Note que $t<x$, (mas não, necessariamente, $t\geq a$).

Figura 2: reta $R$ passando pelos pontos $(t, 0)$ e $(x, F(x))$, onde $t = x -\tfrac{F(x)}{f(x)}$.
Agora, considere um ponto $p\in [a,x)$ e seja $k$ a abscissa do ponto no qual a reta horizontal $y=F(p)$ intersecta a reta $R$ (veja figura 3).
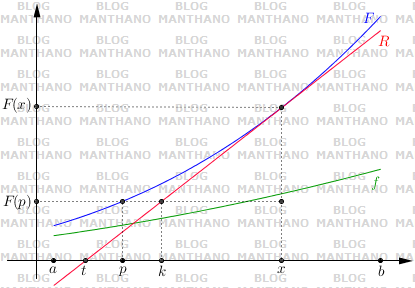
Figura 3: a reta $y = F(p)$ intersecta a reta $R$ no ponto $(k, F(p))$.
Na nossa figura, obtivemos $k>p$. Verifiquemos que, de fato, isto sempre ocorre. Para tanto, vamos nomear os pontos do seguinte modo: $G=(x,F(x))$, $M=(x,F(p))$, $K=(k,F(p))$, $X=(x,0)$ e $T=(t,0)$ (veja figura 4).

Figura 4: alguns pontos nomeados.
Note que os triângulos $GMK$ e $GXT$ são semelhantes. Deste modo, $\tfrac{GM}{MK}=\tfrac{GX}{XT}$, ou seja,
$$\frac{F(x)-F(p)}{x-k}=\frac{F(x)}{x-t}=\frac{F(x)}{x-\left(x-\frac{F(x)}{f(x)}\right)}=f(x)$$
Portanto,
$$x-k=\frac{F(x)-F(p)}{f(x)}.$$
Por outro lado, pela própria definição da $F$, concluímos que $F(x)-F(p)<f(x)(x-p)$ (veja a figura 5).

Figura 5: Note que $F(x) − F(p)$ é a área sombreada e $f(x)(x − p)$ é a área do retângulo destacado. Logo $F(x) − F(p) < f(x)(x − p)$.
Segue-se que
$$x-k=\frac{F(x)-F(p)}{f(x)} <\frac{f(x)(x-p)}{f(x)}=x-p$$
Assim, $k>p$.
Deduzimos, então, que $(p,F(p))$ não está sobre a reta $R$ (pois o único ponto com ordenada $F(p)$ que está sobre $R$ tem abscissa igual a $k$). Como $p\in [a,x)$ foi tomado arbitrário, concluímos que, à esquerda de $x$, o gráfico de $F$ se encontra localizado acima da reta $R$. Um argumento análogo permite mostrar que o mesmo fenômeno ocorre à esquerda do ponto $x$. Assim, a reta $R$ “toca” o gráfico de $F$, mas não o “corta”. Ou seja, $R$ tangencia $F$ no ponto $(x,F(x))$. Portanto, $F'(x)$ é dada pela inclinação da reta $R$, ou seja,
$$\frac{d}{dx}\left[\int_a^xf(s)ds\right]=\frac{d}{dx}F(x)=F'(x)=\frac{GX}{XT}=$$
$$=\frac{F(x)}{x-t}=\frac{F(x)}{x-\left(x-\frac{F(x)}{f(x)}\right)}=f(x).$$
Isto finaliza a demonstração geométrica do primeiro teorema fundamental do cálculo, para o caso particular em que $f$ é crescente e positiva.
O 2º TFC (a parte que nos fornece uma fórmula para o cálculo de integrais definidas) também possui uma versão geométrica provada por Isaac Barrow na mesma obra (Proposição 19, Lecture XI). Poderá ser que, futuramente, a exporemos aqui no BLOG MANTHANO.
Desafio para o leitor: o leitor deve ter percebido que o ponto$ t$ brotou no meio da argumentação sem qualquer justificativa e desempenhou um papel fundamental. A pergunta que fica é a seguinte: como "adivinhar" que escolher $t = x -\tfrac{F(x)}{f(x)}$ funciona? O fato é que há uma motivação geométrica para esta escolha, a qual Barrow não comenta na sua demonstração e que, por hora, deixamos para o leitor investigar.
O 2º TFC (a parte que nos fornece uma fórmula para o cálculo de integrais definidas) também possui uma versão geométrica provada por Isaac Barrow na mesma obra (Proposição 19, Lecture XI). Poderá ser que, futuramente, a exporemos aqui no BLOG MANTHANO.
Referências: Livro The Geometrical Lectures of Isaac Barrow, de J. M. Child e site WolframAlpha.
Erros podem se relatados aqui.
PS.: Feliz natal e próspero ano novo a todos os leitores!



















Este comentário foi removido pelo autor.
ResponderExcluirOlá Multiplicador Pedro, bom dia!
ResponderExcluirDesejo a você e a sua família muita sucesso em 2014!
Seu blog foi mencionado no Educadores Mutiplicadores, saiba o motivo:
http://www.educadoresmultiplicadores.com.br/2014/01/educadores-multiplicadores-de-mes-de.html
Abraços,
Irivan Rodrigues