Considere o conjunto $\mathbb{N}$ que contém todos os números naturais e o conjunto $\mathbb{P}$ que contém todos os números pares:
\mathbb{N}&=\{1,2,3,4,5,6,7,8,9,10,11,...\}\\\\
\mathbb{P}&=\{2,4,6,8,10,12,14,16,18,...\}\end{aligned}$$Qual destes dois conjuntos possui mais elementos?
Podemos pensar da seguinte maneira: os números naturais se dividem entre pares e ímpares. Assim, o conjunto $\mathbb{P}$ é apenas uma parte do conjunto $\mathbb{N}$ e, portanto, o conjunto dos naturais possue mais elementos. Estamos, aqui, fazendo uso da ideia intuitiva de que "o todo é maior do que a parte".
Mas também podemos pensar: ambos são infinitos! Portanto, ambos possuem a mesma quantidade, que é infinita.
Cada resposta acima, olhada isoladamente, parece fazer sentido intuitivo. Entretanto, tento em vista que uma contradiz a outra, não é possível que ambas estejam corretas. Temos, portanto, um impasse para resolver: dados dois conjuntos infinitos, como decidir qual deles possui mais elementos?
Observação: no que se segue, "comparar" dois conjuntos significa "comparar relativamente à quantidade de elementos que eles possuem". Ou seja, significa dizer se eles possuem a mesma quantidade de elementos ou se um deles possui mais do que o outro.
Voltemos para a questão: como decidir, entre dois conjuntos infinitos, qual possui mais elementos? Bom, parece uma boa ideia tentar imitar o que fazemos com conjuntos finitos. Mas como é que comparamos conjuntos finitos? Vejamos, suponha que alguém lhe peça para verificar se uma sala de aula possui mais alunos ou mais cadeiras. Como você procederia? Bom, há pelo menos dois modos.
- Em um deles você vai até a sala, conta o conjunto de cadeiras obtendo um determinado número, digamos que seja $m$. Em em seguida, você conta o conjunto de alunos obtendo outro número, vamos chamá-lo de $n$. Por fim você compara os resultados (ou seja, compara $m$ com $n$) e concluí o que é que existe em maior quantidade. Se $n = m$ você dirá que há tantos alunos quanto cadeiras; se $n < m$ você dirá que há mais cadeiras; se for $n > m$ você dirá que há mais alunos. Certamente este procedimento não funciona para conjuntos infinitos, pois jamais conseguiríamos contar os elemento de um conjunto infinito. De fato, conjuntos infinitos são isso: conjuntos cujos elementos não podem ser contados.
- O outro modo é o seguinte: você vai até a sala e verifica se há cadeiras vazias, alunos de pé ou se nenhuma destas duas possibilidades ocorre. Se houver cadeiras vazias você dirá que há mais cadeiras; se houver alunos de pé você dirá que há mais alunos; se não sobrarem cadeiras e nem houver alunos em pé você dirá que há tantos alunos quanto cadeiras. O interessante é que, neste segundo modo, você não precisa determinar quantos elementos possui os conjuntos de cadeiras e de alunos. Ou seja, a grande sacada é que você será capaz de dizer qual dos dois conjuntos possui mais elementos sem efetuar contagem alguma.
Analisemos mais detidamente este procedimento. Quando você chega na sala de aula, há três casos.
CASO I - Há mais alunos do que cadeiras

CASO II - Há mais cadeiras do que alunos

CASO III - Há tantos alunos quanto cadeiras

Note que temos dois conjuntos e uma correspondência entre eles. Temos, portanto, os ingredientes perfeitos para falarmos em função. Vamos então pensar numa função $f$ que a cada aluno associa uma cadeira. O domínio será o conjunto de alunos e o contradomínio será o conjunto de cadeiras. Nesta linguagem, os três casos podem ser assim traduzidos:
CASO I - $f$ não é injetiva

CASO II - $f$ não é sobrejetiva

CASO III - $f$ é bijetiva

Obviamente, é o terceiro caso que traduz a nossa intuição do que significa ter o mesmo número de elementos. Assim, a partir destas considerações, podemos atribuir significado para a expressão “mesmo número de elemento” do seguinte modo: o conjunto de alunos e o conjunto de cadeiras possuem o mesmo número de elementos se existir uma bijeção entre eles. Ou, de modo mais geral:
Dados os conjuntos $X$ e $Y$, dizemos que eles têm o mesmo número de elementos quando existe uma função bijetiva de $X$ em $Y$
Uma observação importante é que a definição acima elimina por completo a necessidade de contar os elementos dos conjuntos a fim de compará-los e, por conseguinte, nada impede que ela seja aplicada aos conjuntos infinitos (os quais, como já dissemos, não podem ser contados no sentido matemático usual do termo).
Outra observação é a seguinte: do ponto de vista intuitivo, do mesmo modo que esta definição de “número de elementos de um conjunto” faz sentido para conjuntos finitos, ela também faz quando eles são infinitos. De fato, definir uma função bijetiva de $X$ em $Y$ equivale a “formar duplas” . Quando $X$ e $Y$ passam de finito para infinito, a única coisa que muda é que existirão infinitas duplas. A noção de que os conjuntos possuem a mesma quantidade de elementos (isto é, de que nem sobra em um e nem falta no outro) permanece inalterada. É, portanto, esta noção que adotaremos para comparar conjuntos infinitos.
Estamos, agora, em condições de comparar os conjuntos $\mathbb{N}$ e $\mathbb{P}$. De acordo com o que acabamos de ver, poderemos concluir que eles possuem o mesmo número de elementos se existir uma bijeção de $\mathbb{N}$ em $\mathbb{P}$. Isto significa que seremos capazes de formar duplas de números, tais que um membro da dupla está em $\mathbb{N}$ e o outro está em $\mathbb{P}$. Além disso, ninguém de $\mathbb{N}$ e ninguém de $\mathbb{P}$ poderá ficar sozinho.
A maneira mais natural de tentarmos formar estas duplas é colocando:
- o primeiro número natural com o primeiro número par;
- o segundo número natural com o segundo número par;
- o terceiro número natural com o terceiro número par, e assim por diante.
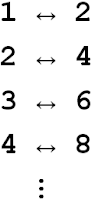
É claro que esta correspondência forma duplas. Além disso, ninguém está sozinho em $\mathbb{N}$, pois podemos determinar a dupla de cada natural $n$ - a qual é o número par $2n$. Também ninguém está sozinho em $\mathbb{P}$, pois podemos determinar a dupla de cada número par $m$ - a qual é o natural $m/2$. Assim, esta correspondência defini uma bijeção de $\mathbb{N}$ em $\mathbb{P}$. Segue que eles possuem o mesmo número de elementos. Ou seja:
Existem tantos números pares quanto números naturais!
Isto é surpreendente e nos mostra que quando lidamos com o infinito, nem sempre o todo é maior do que a parte.
Acabamos de comparar o conjunto dos números pares com o conjunto dos números naturais. Mas e o que dizer sobre outros conjuntos infinitos? Por exemplo, o intervalo aberto $(0,1)$ também é um conjunto infinito. Será que ele também possui a mesma quantidade de elemento do que $\mathbb{N}$? Se a resposta for sim, então existe uma função bijetiva de $\mathbb{N}$ em $(0,1)$. Ou seja, se a resposta for sim, existe uma maneira de formar duplas entre os elementos de $\mathbb{N}$ e $(0,1)$.
Ao contrário do que aconteceu com o conjunto dos números pares, não temos uma sugestão muito natural de como proceder para formar duplas de naturais com os elementos de $(0,1)$. Mas vamos supor que seja possível e digamos que, após muito tentar, tenhamos conseguido. Vamos imaginar que as duplas são as seguintes:
.png)
A fim de concluir que esta correspondência defini uma bijeção, precisamos constatar que cada número do intervalo $(0,1)$ forma dupla com algum número natural. Mas considere o número $x$ construído da seguinte maneira: $x=0,d_1d_2d_3d_4...$, onde os dígitos $d_1,\;d_2,\;d_3...$ são escolhidos da seguinte maneira:
- $d_1$ é diferente da primeira casa decimal do número que forma dupla com $1$;
- $d_2$ é diferente da segunda casa decimal do número que forma dupla com $2$;
- $d_3$ é diferente da terceira casa decimal do número que forma dupla com $3$;
E de um modo geral:
- $d_n$ é diferente da enésima casa decimal do número que forma dupla com $n$;
No nosso exemplo, tem que ser $d_1\neq 3$, $d_2\neq 5$, $d_3\neq 8$, etc. Uma possibilidade é colocar $x=0,4261...$.
Como $x$ é da forma "zero vírgula alguma coisa" eles está no intervalo $(0,1)$. Entretanto, ele não forma dupla com nenhum número natural. De fato, em virtude do modo como $x$ foi construído concluímos que:
- ele não pode formar dupla com $3$, pois a terceira casa decimal de $x$ é diferente da terceira casa decimal do número que forma dupla com $3$;
- ele também não pode formar dupla com $20$, pois a vigésima casa decimal de $x$ é diferente da vigésima casa decimal do número que forma dupla com $20$;
- ele também não pode formar dupla com $1000007$, pois a bilionésima sétima casa decimal de $x$ é diferente da bilionésima sétima casa decimal do número que forma dupla com $1000007$;
- etc., etc., etc..
De um modo geral, $x$ não pode formar dupla com número natural algum. O argumento acima ilustra que, dada uma tentativa de formar duplas entre $\mathbb{N}$ e $(0,1)$, sempre podemos encontrar um número de $(0,1)$ que está sozinho (em outros termos: nenhuma função de $\mathbb{N}$ em $(0,1)$ é sobrejetiva). Isto significa que sempre irá sobrar elementos em $(0,1)$, ou seja, o intervalo $(0,1)$ possui mais elementos do que o conjunto $\mathbb{N}$. Segue que:
Nem todo conjunto infinito possui a mesma quantidade de elementos!
Certamente, se trocamos "infinito" por "finito" na frase acima, ela soa absolutamente natural. Mas talvez o leitor concorde que nossa intuição parecia esperar o contrário para os conjuntos infinitos.
Assim como $(0,1)$ possui mais elementos do que $\mathbb{N}$, o conjunto $\mathbb{R}$ dos números reais também possui. Neste contexto surge uma pergunta: será que existe um conjunto infinito $X$ tal que $X$ tenha mais elementos do que $\mathbb{N}$ e, ao mesmo tempo, menos elementos do que $\mathbb{R}$?
A hipótese de que não existe um conjunto $X$ com esta propriedade é chamada de "Hipótese do Contínuo" e é devida ao matemático alemão George Cantor (1845-1918). Esta é uma questão que constava na famosa lista dos 23 problemas apresentados pelo matemático alemão David Hilbert (1862-1943) na virada do século XIX.


Georg Cantor David Hilbert
O interessante sobre esta hipótese é que, no contexto da atual teoria axiomática dos conjuntos, o matemático austríaco Kurt Gödel (1906-1978) provou que não é possível provar que ela é falsa enquanto que o matemático americano Paul Cohen (1934-2007) provou que é não é possível provar que ela é verdadeira.


Kurt Gödel Paul Cohen
A hipótese do contínuo ilustra, então, que existem afirmações na matemática que não podem ser demonstradas e nem refutadas. Ela é um exemplo daquilo que se chama "indecidível".
Espero que tenham apreciado a leitura.
Referências: Teoria Ingênua dos Conjuntos (Paul Halmos); Curso de Análise (Elon Lages Lima), Curso de Análise Real (Cassio Neri e marco Cabral). Retratos extraídos daqui.
Notas finais:
- O argumento utilizado para provar que nenhuma função de $\mathbb{N}$ em $(0,1)$ é sobrejetiva é conhecido como "argumento da diagonal de Cantor". A intenção foi passar a ideia de como ele funciona, de modo que nem todos os detalhes envolvidos foram explicitados.
- Tecnicamente, conjuntos que possuem tantos elementos quanto $\mathbb{N}$ são chamados de "conjuntos enumeráveis" e conjuntos que possuem mais elementos do que $\mathbb{N}$ são chamados de "conjuntos não enumeráveis". Assim, vimos que $\mathbb{P}$ é enumerável enquanto que $(0,1)$ é não enumerável;
- Em geral, quando o assunto é conjunto infinito, não se diz "quantidade de elementos" mas sim "cardinalidade". Assim, o que vimos foi que $\mathbb{N}$ e $\mathbb{P}$ possuem a mesma cardinalidade enquanto que $\mathbb{N}$ e $(0,1)$ não possuem.
- O leitor pode se perguntar se existe algum conjunto infinito com menos elementos do que o conjunto dos números naturais. A resposta é não. Qualquer conjunto infinito tem, no mínimo, tantos elementos quanto $\mathbb{N}$. Fatos desta natureza geralmente são estudados nos cursos de análise.
Erros podem ser relatados aqui.



















Olá Multiplicador Pedro, felicidades para toda sua casa!
ResponderExcluirDia 05/07 estamos completando um ano de atividades. Vou confessar que não é nada fácil ter que organizar todas as postagens constantemente, atender inúmeros pedidos em off, porém fazemos com muito carinho e procuramos fazer o nosso melhor da forma que é possível para nós, em virtude de tempo e cansado do trabalho.
No momento estamos de férias do trabalho e, para aproveitar esse tempo extra (as férias) queremos pedir a você em especial que convide outros educadores para conhecer o Projeto Educadores Multiplicadores. Assim nossa festa no dia 05/07 será ainda mais abrilhantada. Vamos alargar nossas fronteiras! Todos pela Educação!
DIVULGUE PARA SEUS AMIGOS PROFESSORES o EDUCADORES MULTIPLICADORES.
A parceria é exclusiva para blogs de Educadores/Professores que escrevem conteúdos ligados diretamente à Educação.
Por de falta de tempo, pedimos desculpas pela demora em lhe visitar.
.
Abraços, fiquemos na Paz de Deus e até breve. Agradecemos sua compreensão!
Atenciosamente,
IRIVAN
Com relação a questão de existir um conjunto com mais elementos que N e menos que R, creio que seria o conjunto dos racionais Q, não? Se não por que não há como provar isso?
ResponderExcluirCertamente existem elementos em $\mathbb Q$ que não estão em $\mathbb N$ e existem elementos em $\mathbb R$ que não estão em $\mathbb Q$. Nesse sentido, poderíamos pensar que $\mathbb Q$ tem mais elementos do que $\mathbb N$ e menos do que $\mathbb R$. Porém, quando formalizamos a noção de "quantidade de elementos" para conjuntos infinitos, concluímos que $\mathbb Q$ e $\mathbb N$ possuem a mesma quantidade de elementos (veja Obs. 1 abaixo). Portanto, a resposta para a sua primeira pergunta é "não".
ResponderExcluirNa segunda pergunta, você pergunta porque não é possível provar que "não existe conjunto com mais elementos do que $\mathbb N$ e menos do que $\mathbb R$?" Se sim, a reposta é porque tanto esta afirmação quanto a sua negação é consistente com os axiomas "usuais" da teoria dos conjuntos (veja Obs. 2 abaixo).
Obs. 1: Dois conjuntos "possuem a mesma quantidade de elementos" quando existe uma bijeção entre eles (i.e., quando podemos "formar duplas" de seus elementos). Na prática, isso significa que um conjunto terá a mesma quantidade de elementos de $\mathbb N$ se for possível fazer uma lista que contenha todos os seus elementos. Como é possível listar todos os elementos de $\mathbb Q$, concluímos que $\mathbb Q$ e $\mathbb N$ possuem a mesma quantidade de elementos.
Obs. 2: O fenômeno é semelhante ao que ocorre na geometria: é possível provar que "por um ponto fora de uma reta $r$ passa uma única reta que é paralela a $r$"? No contexto da "geometria absoluta", não. Isto significa que tal afirmação, tanto quanto sua negação, é consistente com os axiomas da geometria absoluta. Assim, na geometria absoluta, podemos escolher considerar esta afirmação verdadeira ou considerá-la falsa. Fazendo a primeira escolha, obtemos a "geometria euclidiana usual". Fazendo a segunda escolha, obtemos as chamadas "geometrias não euclidianas".
Pedro R.