Comutatividade no infinito

O objetivo desta postagem é apresentar aos leitores do BLOG MANTAHNO algo que, para mim, pareceu sobremodo surpreendente quando descobri.

A propriedade comutativa da multiplicação é aquela que diz o seguinte: se a e b são números reais, então

a×b = b×a

Por exemplo: 2×4 = 4×2 (ambos os lados da igualdade valem 8). Resumidamente, tal propriedade diz que a ordem dos fatores não altera o produto.

A propriedade comutativa da adição, por sua vez, diz algo parecido: a ordem das parcelas não altera a soma. Ou, de modo mais preciso, se a e b são números reais, então

 a + b = b + a

Especificar que a e b são números reais é de fundamental importância neste caso, pois se não esclarecermos bem quem são os fatores (e qual é a operação envolvida) corremos o risco de a propriedade não funcionar (acima ficou implícito que × e + representam, respectivamente, as operações de multiplicação e de adição usuais – as quais bem conhecemos desde a época em que chamávamos a professora de tia).

Ilustremos o que acabamos de dizer: a afirmação "a ordem dos fatores não altera o produto" é falsa se os fatores forem matrizes e o produto for o resultado da multiplicação de matrizes. Por exemplo:

Por outro lado, a afirmação "a ordem das parcelas não altera a soma" continua válida mesmo que estejamos nos referindo às operações matriciais. Mas voltando ao conjunto dos reais, a propriedade comutativa da adição vale de uma maneira um pouco mais geral: se c também é um real, então

a + b + c = a + c + b = b + a + c = b + c + a = c + a + b = c + b + a

E nada nos impede de acrescentar mais uma parcela, pois ainda assim poderíamos alterar suas ordens (de modo totalmente arbitrário) sem alterar o valor da soma. Na verdade, podemos fazer isso com qualquer número finito de parcelas. Bom, até aqui nenhuma novidade. Todos já estamos acostumados a lidar com estas operações e usufruir destas propriedades.

Mas a pergunta que eu gostaria de apresentar ao leitor é seguinte: o que acontece com a comutatividade da adição se considerarmos um número infinito de parcelas reais? Será que a propriedade comutativa ainda vale? Em outras palavras: será que, se somarmos uma quantidade infinita de números reais, podemos alterar de modo completamente arbitrário a ordem das parcelas sem que o valor da soma seja alterado? (Isso, presumo eu, seja novidade pelo menos para uma parte da população).

A verdade é que, de modo geral, tal propriedade não vale quando estamos lidando com somas infinitas. Como exemplo, consideremos o número  loge⁡(2) expresso como uma soma de infinitas parcelas:

Dividindo ambos os lados por 2:

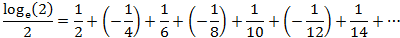
Reescrevendo a soma de modo conveniente:

Somando termo a termo as expressões [I]  e [II]:

Enfim:

O leitor atento poderá notar que as somas [I] e [III] possuem exatamente as mesmas parcelas (o procedimento algébrico serviu para reordená-las). O leitor também poderá notar que, apesar disso, os valores das suas somas são diferentes! (olhando o lado esquerdo das respectivas igualdades, vemos que a primeira vale aproximadamente 0.69 enquanto que, a segunda, vale mais ou menos 1.03). Ou seja, mudamos a ordem das parcelas e o valor da soma não permaneceu o mesmo. Isso mostra que quando o assunto é o infinito as coisas mudam de figura.

OBSERVAÇÃO 1: o texto acima assumiu alguns fatos sem maiores explicações de maneira que alguns leitores (provavelmente) estão se perguntando, dentre outras coisas, o seguinte:

- Como sabemos que  log⁡e(2)  é dado por aquela soma infinita?

- Como sabemos que, quando temos uma igualdade na qual um dos membros é uma soma infinita, podemos efetuar certas operações em ambos os lados sem alterar a validade da igualdade (por exemplo, dividir ambos os lados por 2)?

Para responder de modo detalhado a estas questões, precisamos nos aprofundar um pouco mais nos estudos das “somas infinitas”, ou seja, das séries (tanto numéricas quanto de Taylor). Por isso sugiro aos interessados que pesquisem em livros de Cálculo Diferencial e Integral e/ou Cálculo Numérico e/ou Análise Real. De qualquer modo, dúvidas pontuais podem ser deixadas como comentário que, o mais breve possível, responderei.

OBSERVAÇÃO 2: às vezes, a comutatividade ainda vale mesmo quando a soma tem infinitas parcelas, por exemplo:

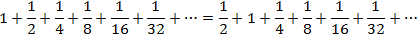
Usando a conhecida fórmula da soma dos termos de uma progressão geométrica infinita, podemos concluir que cada um dos lados da igualdade acima vale 2.

OBSERVAÇÃO 3: embora loge(2) (assim como qualquer outro número real) possa ser expresso como uma soma de infinitas parcelas, nem toda soma de infinitas parcelas representa um número real. Seguem dois exemplos de somas infinitas que não representam número real algum:

1 + 1 − 1 + 1 − 1  + 1 − 1 + 1 − 1 + 1 − 1 + 1 − 1 + 1 − 1 + 1 − 1 + ⋯

OBSERVAÇÃO 4: para encerrar, uma mini nota histórica: o fato ilustrado nesta exposição (isto é, de que quando alteramos a ordem das parcelas de uma soma infinita o seu valor nem sempre permanece o mesmo) foi descoberto pelo matemático francês Augustin-Louis Cauchy em 1833.

Referência: "Curso de Análise Volume 1" de Elon Lages Lima e "Cálculo Volume 1" de Tom M. Apostol.

Erros podem ser relatados aqui.