BLOG MANTHANO: EDO: variáveis separáveis - exercícios resolvidos (passo a passo) / Parte 4

segunda-feira, 29 de agosto de 2011

EDO: variáveis separáveis - exercícios resolvidos (passo a passo) / Parte 4

PROBLEMA:

Sabendo que a população de uma cidade dobra a cada 50 anos, em quantos anos ela será o triplo, admitindo que a razão do crescimento é proporcional ao número de habitantes?

SOLUÇÃO:

Escrevendo matematicamente a informação dada no enunciado do exercício (”a razão do crescimento é proporcional ao número de habitantes”) obtemos a seguinte equação diferencial:

$\frac{dP}{dt}=kP$

Onde dP/dt representa a razão do crescimento, P = P(t) é o número de habitantes (em função do tempo t) e k é a constante de proporcionalidade.

Analisando essa equação, percebemos que ela é separável. Separando as variáveis:

$\frac{dP}{p}=kdt$

Integrando ambos os lados:

$\int \frac{dP}{p}=\int kdt$

Pelas regras básicas de integração:

$\ln(P)=kt+C$

Tomando a exponencial de ambos os lados e aplicando algumas propriedades de potências:

$e^{ln(P)}=e^{kt+C}$

$P=e^{kt}\cdot e^C$

Sabendo que e^C é uma constante, vamos chamá-la de D (somente para simplificar). Então temos:

$P=e^{kt}\cdot D$

Vamos chamar a população no tempo t = 0 (tempo inicial) de P₀ (população inicial), ou seja, P(0) = P₀. Segue-se disto que:

$P(0)=e^{k\cdot 0}\cdot D\Leftrightarrow P_0=e^0 \cdot D\Leftrightarrow P_0=1\cdot D\Leftrightarrow P_0=D$

Então, em vez de escrever a letra D, vamos usar P₀(pois acabamos de ver que elas são iguais):

$P(t)=e^{kt}\cdot P_0$

Função que descreve o crecimento da popuação.

No enunciado do problema foi dito que a cada 50 anos a população dobra, portanto no tempo t = 50 temos P = 2⋅P₀, ou seja, P(50) = 2⋅P₀.

Vamos substituir esses dados na função que encontramos para deste modo conhecer o valor de k:
$2\cdot P_0=P(50)$
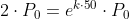
$2\cdot P_0=e^{k\cdot 50}\cdot P_0$
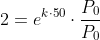
$2 =e^{k\cdot 50}\cdot \frac{P_0}{P_0}$
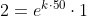
$2 =e^{k\cdot 50}\cdot 1$
$e^{k\cdot 50}=2$
Tomando o logaritmo natural de ambos os lados (e aplicando algumas propriedades):
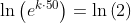
$\ln\left (e^{k\cdot 50} \right )=\ln\left (2 \right )$
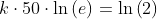
$k\cdot 50\cdot \ln\left (e \right )=\ln\left (2 \right )$
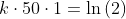
$k\cdot 50\cdot 1=\ln\left (2 \right )$
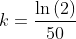
$k=\frac{\ln\left (2 \right )}{50}$
Usando uma calculadora, concluímos que:

$k\cong 0,0138$

Já que conhecemos o valor numérico de k, vamos usar este valor na função que descreve o crescimento da população:

$P(t)=e^{0,138\cdot t}\cdot P_0$

O problema quer saber: Em quantos anos a população será o triplo? Ou seja, qual será o valor de t quando P = 3⋅P₀? Em outras palavras: quer saber o valor de t que satisfaz a seguinte igualdade:

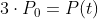
$3\cdot P_0=P(t)$

Substituindo P(t) pela função que acabamos de encontrar:

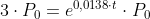
$3\cdot P_0=e^{0,0138\cdot t}\cdot P_0$
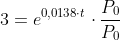
$3=e^{0,0138\cdot t}\cdot \frac{P_0}{P_0}$
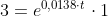
$3=e^{0,0138\cdot t}\cdot 1$
$e^{0,0138\cdot t}=3$

Tomando o logaritmo natural de ambos os lados (e aplicando algumas propriedades):

$\ln\left (e^{0,0138\cdot t} \right )=\ln\left (3 \right )$
${0,0138\cdot t}\cdot\ln\left (e^ \right )=\ln\left (3 \right )$
${0,0138\cdot t}\cdot1=\ln\left (3 \right )$
$t=\frac{\ln\left (3 \right )}{0,0138}$
Usando uma calculadora:

t ≅ 79,6 anos

Portanto, passados (aproximadamente) 79,6 anos a população será o triplo da população inicial.

[Veja mais: Parte 1 / Parte 2 / Parte 3]